基礎理論 - 1.基礎理論 - 2.応用数学 - 7.最適化問題
制約式(制約条件)と呼ばれるいくつかの1次式を満たす変数の値の中で、目的関数と呼ばれる1次関数を最大化または最小化する値を求める方法である。この目的式の最大値、及びそれを実現する変数を求める問題が線形計画問題である。
ある制約条件のもとで利益を最大化したり、コストを最小化するような解を求めることを「数理計画法」と言います。このとき、条件や目的が「1次関数」で表現されるものを「線形計画法」と言います。
いくつかの1次不等式および1次等式を満たす変数の値の中で、ある1次式を最大化または最小化する値を求める方法である。線形計画法では「目的関数」と「制約条件式」から成ります。
「線形計画法」
アローダイアグラムともいう。
作業の日程や工程を管理するための手法。
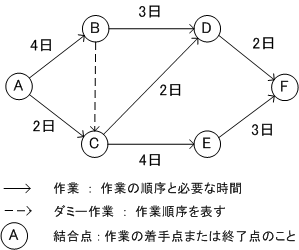
【 ダミー作業 】
CからDとEへの作業は、本来ならAからCの作業の済んだ2日後から開始できるが、BからCのダミー作業があるので、AからBの作業の済んだ4日後からの開始になる。
ダミー作業は、AからCの作業とAからBの作業の両方が終了しないとCからの作業が開始できないことを示す。
【 最早結合点時刻 】(最早開始日)
DからFの作業は、A→B→Dの7日後とA→B→C→Dの6日後の2つの経路があるうちの遅い方の7日後から開始できる。その日を最早結合点時刻という。
求め方は、全体の作業開始日からそれぞれの作業日を足し合わせて計算する。経路が複数ある場合は、もっとも大きい合計を選ぶ。
【 最遅結合点時刻 】(最遅開始日)
Fに到達するまでの作業日数を計算すると、もっとも時間のかかる経路A→B→C→E→Fの11日から、逆算すると
DからFの作業は、作業開始から9日後に開始しても間に合う。このもっとも遅く作業を開始できる日を最遅結合点時刻という。
全体の作業のもっとも時間のかかる日数から引き算をして求める。複数ある場合は、もっとも小さい値を選択する。
【 余裕時間 】
最遅結合点時刻 - 最早結合点時刻 から求められる日数を余裕時間という。
結合点Dの余裕時間は、9 - 7 の2日間になる。
【 クリティカルパス 】
クリティカルパスは、経路の中で最も時間のかかる経路のことを言う。
また、最遅開始日から最早開始日を引いて、余裕期間がゼロの作業を結んだものである。クリティカルパスによって、プロジェクト全体の遅れに直結する作業を把握することができる。
クリティカルパス上の作業に遅延が発生すれば、全作業の完了日数に影響を与える。 逆に、クリティカルパス上の作業を早く終わらせれば、全作業の完了日数を短縮することも可能になる。 そうした意味では、作業進行を管理する上で、最も重要視すべき経路である。
図の場合は、経路A→B→C→E→Fの11日間がもっとも時間のかかる経路なのでクリティカルパスになる。
ボトムアップ方式で小問題の解を順に表を使って積み上げていく問題解決方法である。ある種の最適解を求める問題に適用される方法である。
この方法では、部分的な問題を解決してその解を表に記録していく。より大きな範囲の問題を解決するときは記録された表を参照して解を求め表に記録していき、最終的に問題全体の解を求めるという考え方である。
ある最適化問題を複数の部分問題に分割して解く際に、そこまでに求められている以上の最適解が求められないような部分問題を切り捨てながら解いていく手法である。
問題を分割したときに、「部分の最適化」が全体に適用できることと、そうした最適化の重複が存在していること。こうした問題に対しては動的計画法が適用できる可能性が高い、ということ。
分割統治法がトップダウン的な手法であるのに対し、動的計画法はボトムアップ的な手法といえる。
問題全体を部分問題に分割でき、問題全体の最適化にその部分問題の最適化が利用できる。
- 平成30年度春期 問51 アローダイアグラム
- 平成29年度春期 問51 アローダイアグラム
- 平成29年度秋期 問66 最適化問題
- 平成27年度春期 問54 クリティカルパス
- 平成27年度春期 問78 最適時間
- 平成27年度秋期 問51 アローダイアグラム
- 平成26年度春期 問76 最適化問題
- 平成26年度秋期 問52 アローダイアグラム
- 平成26年度秋期 問74 最適化問題
- 平成25年度秋期 問75 最大利益
www.it-shikaku.jp