基礎理論 - 2.アルゴリズムとプログラミング - 1.データ構造 - 2.データ構造の種類
配列とは、型が同じで変数名が同じである複数の要素をもつデータ構造です。
配列の要素を識別するためには「添字(インデックス)」を使用します。
メモリ上では、配列は順番に並べてデータは格納される。
配列名とデータを識別するための添字(インデック)で構成される。
配列の大きさをあらかじめ決めておかなければならない。
配列にデータを挿入したり削除する場合は手間がかかる
配列の添え字が 1 つのものを 1 次元配列、2 つのものを 2 次元配列という。
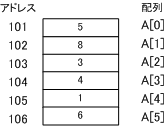
【 多次元配列 】
配列の中に配列が入っており、さらにその中に配列が入っている配列。
二次元配列のさらに次元数が多い配列を指す。
基本的には二次元配列と同じく「配列の中に配列が入っている」のが繰り返されているだけである。
アクセス方法も「[]」をそのまま増やしていけば同様に扱える。
| A [1,1] | A [1,2] |
| A [2,1] | A [2,2] |
| A [3,1] | A [3,2] |
【 静的配列 】
決まった要素数しか格納できない配列を静的配列と言う。
【 動的配列 】
要素数によって自動的にサイズが拡張する配列。可変長配列とも言われる。
【 線形リスト 】
リストは、データを格納する部分と、次のデータの格納されているアドレスを格納する部分を持つ。
データは、数珠つなぎになっている。メモリ上では、順番に並んでいるとは限らない。
線形リストはデータとポインタとが入ったノードまたはセルと呼ばれる要素をポインタでつないだものである。

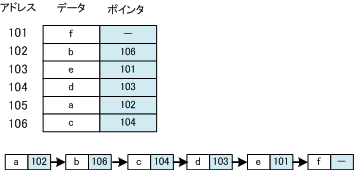
線形リストと配列とを比べたときの、線形リストの利点と欠点は
●利点
・ノードを自由に増やせる
通常、各ノードのためのメモリは、必要とされるときにヒープと呼ばれるメモリ領域に確保される。したがって、プログラム実行時に、メモリ容量の許す限りノードの個数を増やすことができる。
・ノードの挿入削除が簡単
ポインタでノードがつながっているため、データの削除、挿入をしたとき、そのデータをもつノードとその前のノードとに含まれる、次のノードを指すポインタを書き換えるだけで済む。
●欠点
・ノードへのアクセスが面倒
リストにアクセスするには、リストの先頭を指すポインタからリストに入り、ノードを順にたどっていく。したがって、各ノードへのアクセスに手間がかかるのが、欠点である。
【 単方向リスト(線形リスト) 】
次のデータへのポインタだけを持つリスト。
単方向リストでは、データをアクセスする場合には、先頭から順にデータをたどっていくしか方法がない。
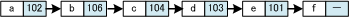
【 双方向リスト 】
前のデータへのポインタと次のデータへのポインタを持つリスト。
双方向リストでは、先頭からと、後方からの両方でデータをたどることができる。

【 環状リスト(循環リスト) 】
単方向リストの最後のデータが先頭のデータへのポインタを持つリスト。
循環リストは先頭や最後尾といったものが存在しないリストと考えることもできる。循環リストはデータ格納用バッファの管理によく使われ、1つのノードを使っているスレッド(やプロセス)が他のノードを全て参照したい場合などに便利である。
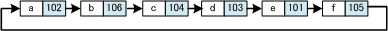
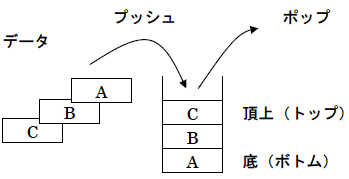
【 スタック 】
リストまたは配列の特殊な場合で、データの出し入れがリスト(配列)の一方でのみ行われます。
スタックへのデータの格納をプッシュ(PUSH)、スタックからデータを取りだすことをポップ(POP)と言います。
データは、後に入れたものが先に取りだされるLIFO方式です。
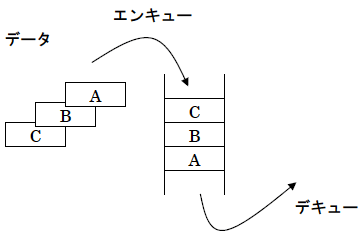
【 キュー 】
リストや配列の特殊な場合で、データの出し入れがリスト(配列)の先頭と最後尾の両方で行われます。
キューにデータを格納することをエンキュー(ENQUEUE)、キューからデータを取りだすことをデキュー(DEQUEUE)と言います。
データは後に入れたものが先に取りだされるFIFO方式です。
- (単純)キュー
キューの決められた一端からデータを追加(エンキュー)し、 もう一端からデータを取り出(デキュー)します。 - ディーキュー( deque : double ended queue)
キューのどちらの端にもデータの追加をすることができ、 また、どちらの端からもデータを取り出すことができる特別なキューです。
ディーキューの実装は双方向リストを使います。双方向リストでは、リストの両端の 追加および削除が単方向リストよりも効率よくできるためです。
【 木 】
木は、データの階層関係を表現するのに向いている。
一番根元の部分の要素を根、要素と要素をつなげる部分を枝、途中の要素部分を節、枝の一番先端にある要素を葉とよぶ。
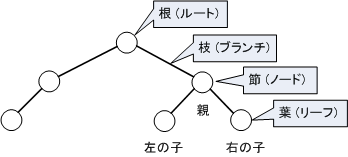
枝の上側の節を親、下側の節を子と呼ぶ場合もある。
また、子から下にさらに枝があり木となっている場合は、部分木と呼ぶ。
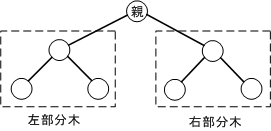
【 2分木 】
親の節につながっている子が2つ以下である木
【 完全2分木 】
「根から深さの小さい順に、かつ同じ深さでは左から順に節を詰めた2分木(木の深さがすべて等しい)」のこと。
(一般には、階層数の差が1以下の場合を含めて、完全2分木と呼ぶ。)
ノードの個数が2n-1個のとき、すべてのノードについて左右の子孫のノードの個数が同じということを満たす。
【 バランス木 】
平衡木ともいいます。どの葉に至るまでも枝の数(木の深さといいます)がほぼ等しい木をいいます。
バランス木には、AVL木とB木がある。
【 AVL木 】
AVL木とは、2分木の中でも、どの節点においても、左右の部分木の高さの差が1以下の平衡(バランスが取れた)木のことである。
2分木に何の工夫もなしに単純にデータを追加していくと、最悪の場合には、一本道の木構造になってしまい、木とする意味がなくなる。そこで、左右の木の偏りを修正する手法として、データの追加・削除で高さの差が2以上となりバランスが崩れると、木の再構成を行うことでAVL木を構築するという手法が考案された。
【 B木 】
全ての葉の深さが同じである木構造をいいます。バランス多分木ともいわれます。
子の最大数がm、最小数がm/2となる多分木
根から葉までの深さは一定。
【 順序木 】
節の値に順序がある木構造
【 多分木 】
節から分岐する枝が2以上の木構造
【 探索木 】
データを探索するのに適している木構造
【 2分探索木 】
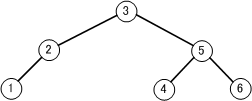
2分探索木は、各節点がもつデータについて、常に左の子<親<右の子となっている2分木
【 ヒープ 】
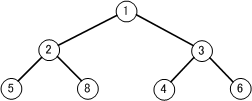
すべての節で親と子の間に一定の大小関係が成り立つ完全2分木のこと。
親≧子 または、親≦子 が常に成り立つ。同じレベルでは左の子から順に詰めてセットされる。
左右の子の大小は問わない。
ヒープでは、根が最小値(または最大値)になる。
節点データを処理するには、木をたどる必要がある。
木の節点をたどることを走査という。(巡回ともいう)
走査方法に深さ優先順と幅優先順がある。
1.幅優先順
ルートから浅い節を先に走査して、同じレベルの節をすべて走査したら、次に深い節を順に走査する。
キューを使う
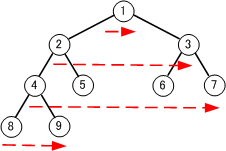
2.深さ優先順
ルートから順に深くなるように走査して、一番深いところまで走査したら、また、上から順に深くなるように走査していく。
一旦は一番深い節まで走査する。
スタックを使う
深さ優先探索ですべての節をもれなく走査する方法に前順・中間順・後ろ順の3種類ある。
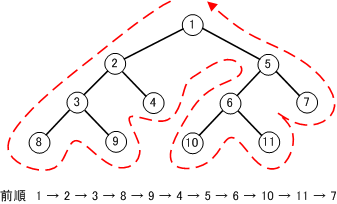
【 前順 】
先行順や行きがかり順ともいう。
節点→左部分木→右部分木の順で走査する。
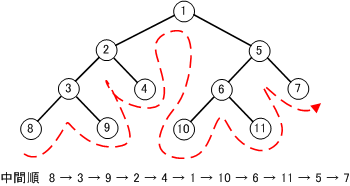
【 中間順 】
通りがかり順ともいう。
左部分木→節点→右部分木の順で走査する。
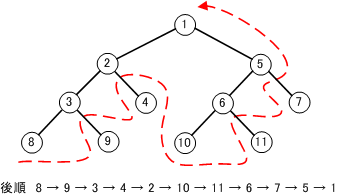
【 後順 】
後行順や帰りがけ順ともいう。
左部分木→右部分木→節の順で走査する。
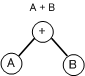
後順を使うと逆ポーランド記法になおせる。
式は木になおすと
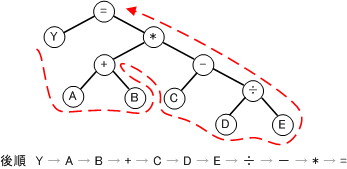
Y=(A+B)*(C-(D÷E))は
- 平成30年度秋期 問05 キュー 待ち行列
- 平成28年度春期 問05 2分木
- 平成28年度春期 問06 配列
- 平成28年度秋期 問06 2分探索木
- 平成27年度春期 問05 キュー
- 平成26年度春期 問06 2分木
- 平成26年度春期 問07 キュー スタック
- 平成26年度秋期 問05 スタック
- 平成25年度春期 問05 2分探索木
- 平成25年度秋期 問05 キュー 待ち行列
www.it-shikaku.jp