顧客がサービスを受けるために行列に並ぶような確率的に挙動するシステムの混雑現象を数理モデルを用いて解析することを目的とした理論である。応用数学のオペレーションズ・リサーチにおける分野の1つに数えられる。
待たずにサービスを受けることができる確率や、人が並んでいる長さ、サービスを受ける平均時間などを計算する理論。

【 M/M/1 モデル 】

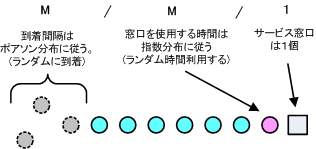
人が到着するのがランダム、サービス時間がランダム、サービス窓口の個数は1つの場合の待ち行列理論。

• システム内の滞留可能数 ＝ 無限大
• サービスを受ける窓口の数 ＝ 1 個
• 1 件あたりのサービス時間 ＝ 指数分布に従う
• 単位時間当たりの到着数 ＝ ポアソン分布に従う
• 到着順にサービス
• 割り込みはない
• 並んだ客は立ち去らない

1. 平均到着率 : λ
   単位時間あたりに到着する人数(タスク)のこと
   

2. 平均サービス率 : μ
   単位時間当たりの処理件数
   ひとつの窓口でどれだけサービスを処理出来るかの割合
   

3. 平均利用率 : ρ
   ρ ＝ λ / μ ＝ λ・Ts
   窓口がどれだけ利用されているかの割合
   

4. 利用していない確率 ＝ 1 － ρ
   

5. 平均サービス時間(TS:Time Service) : Ts
   Ts ＝ 1 / μ
   窓口において、要求されたサービス１件を処理するのにかかる時間
   並んでいる人を処理する時間
   

6. 平均待ち時間(TW:Time Wait) : Tw
   Tw ＝ ( ρ / ( 1 － ρ ) ) × Ts
   待ち行列に並んで、サービス処理が開始されるまでの待ち時間 サービスを受けるまでの時間
   

7. 平均到着間隔(TA:Time Arrival) : Ta
   Ta ＝ 1 / λ
   到着してから次に到着するまでの平均時間
   

8. システム内の平均客数(長さ) L ＝ ρ / ( 1 － ρ )
   

9. サービス待ち中の客数の平均人数 : Lq
   Lq ＝ L － ρ ＝ ρ² / ( 1 － ρ )
   

10. 平均応答時間 : W
    W ＝ 平均待ち時間 ＋ 平均サービス時間 ＝ Tw ＋ Ts
    ＝ L × 1 / λ ＝ 1 / ( μ － λ )
    システム内にいる平均時間
    

11. サービスを受けるために待つ平均待ち時間 : Tw
    Tw ＝ W － 1 / μ ＝ ρ / ( μ － λ ) ＝ λ / μ ( μ － λ )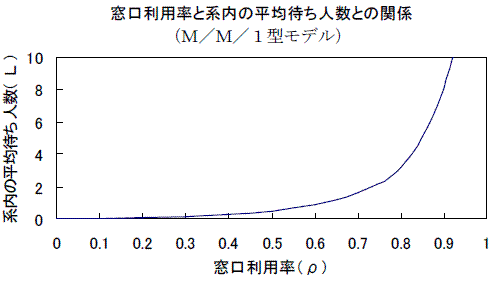
    
    

    

1. 平成27年度春期　問14　　CPUの使用率と平均応答時間の関係　ポアソン分布
2. 平成11年度秋期　問70　　待ち行列　ポアソン分布