基礎理論 - 1.基礎理論 - 2.応用数学 - 5.グラフ理論
Last Update : January 02 2021 16:00:15
a. グラフ理論
ある要素を関連付けて整理したり、分析したりするために、要素間のつながりをグラフとして分析する手法のこと。
いろいろな要素を点に置き換え、その関連性を辺で結び特徴を分析する。
b. グラフとは
グラフ(G)は、有限個の点(V)と辺(E)から構成されます。点はグラフを構成する各頂点で、辺は頂点同士を結びます。ひとつの点についている辺の数を次数という。一般に、グラフはG=(V,E)と定義します。
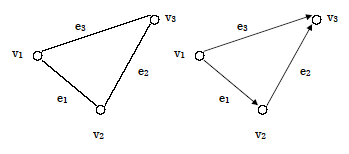
辺に向きがないものを無向グラフ(上図左)、向きがあるものを有向グラフ(上図右)と言います。
有向グラフの場合、点に入ってくる辺の数を入次数といい、点から出ていく辺の数を出次数という。
この図の場合、e1=(v1,v2),e2=(v2,v3),e3=(v1,v3)と表記します。一般に、e=(vi,vj)のvi,vjをそれぞれ端点と言います。
- グラフの次数の合計は偶数になる。
- グラフは奇数の次数を持つ点が偶数個ある。
c. 隣接行列
隣接行列はグラフを表現するために用いる行列である。
行は自分の点を表し、列は相手の点を表す。
点と点に辺がつながっている場合は1、つながっていない場合は0とする。
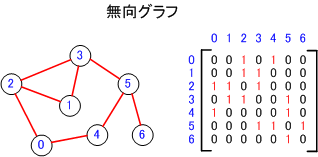
- 無向グラフの場合(重みづけのない場合)
お互いがつながっている場合、行の中で相手の点の位置に1をセットする。つながっていない場合は、0をセットする。
無向グラフの場合、左上と右下を結んだ線を中心として対称となる。
- 有向グラフの場合(重みづけのない場合)
自分の点から相手の点に向かっている場合は、行の相手の点の位置に1をセットする。 自分の点に来ている場合は、0をセットする。 ただし、自分自身の点から自分自身に向かっている(自己ループ)場合は、自分自身に1をセットする。 また、つながっていない場合も0をセットする。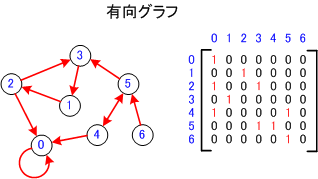
d. ダイクストラ法による最短経路探索
スタート地点から距離の近い地点から順に最短経路を確定させ、その地点に隣接する地点の最短経路を必要に応じて更新していくことで、スタート地点から各地点への最短経路を求めていきます。
[ 例題 ]
- 平成24年度春期 問03 隣接行列
- 平成18年度春期 問11 グラフ
www.it-shikaku.jp