正確な解を求めることができない数学上の問題を近似的に解く方法のこと

二分法（ Bisection method ）の原理
二分法は方程式 f(x) ＝ 0 の解を求める方法である。手順 としては以下のようになる。

1. 解を含む区間の算出
   f(a) ＜ 0、f(b) ＞ 0を満たすような変数 a ，b を決める。
   または
   f(a) × f(b) < 0
   を満たすa,bを決める。
   
2. 算出した区間の中間点を計算する。
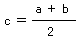   を計算して f(c) の値を計算する。
   
3. 算出した中間点を使って、新しい区間を算出する。
   f(c) ＜ 0 ならば a を c に置き換え、f(c) ＞ 0 ならば b を c に置き換える。これで、正負が変化する個所つまり根がある領域を半分に狭めることになる。
   
4. 2，3 を繰り返して、a ， b の範囲を狭めていく。

これが二分法の考え方である。図で描くと以下の図の 図 1 → 図 2 → 図 3 → 図 4 のような感じになる。

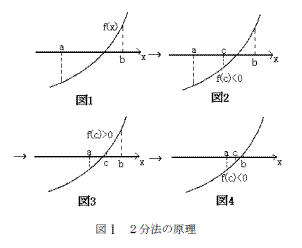
二分法は、計算は遅いが確実に根のある領域を狭めていって解を求めることができる方法である

補間とは、与えられた複数の点をすべて通る曲線において、ある x 値に対して その曲線上の y 値を求める計算のことです。
異なる複数の点を通る多項式を求め、離散的な（連続でない、とびとびの）データから値を推測する方法をラグランジュ補間法という。

ニュートン法は方程式 f(x) ＝ 0 の解を求める方法である。手順 としては以下のようになる。

1. 初期値 x ＝ x₀ を決める
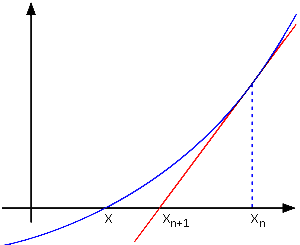
2. x ＝ x₀における　y ＝ f(x)の接線を引き、この接線と y ＝ 0 ( x 軸 ) の交点を x₁とする。つまり、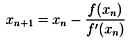を計算する。
3. 2 を繰り返して接線を引いていく。

f'(x_n)はf(x_n)の導関数と呼ぶ。
[導関数の求め方]
式の指数部を前に持ってきて次数を1つ下げる
Ex. f(x) = x²の導関数は
f'(x) = 2x

Ex. f(x) = 2x³ + 4x² + 5 の導関数は
f'(x) = 6x² + 8x

ニュートン法で√2を解く
x = √2
両辺を2乗する。
x² = 2
x² - 2 = 0
f(x) = x² - 2
このf(x)の導関数は
f'(x) = 2x
になる

ニュートン法の関係式について当てはめると次の様になる

ここでx₁の値を適当に5と仮定してn=5まで計算をしてみる

√2の真の値は1.414...となるので、計算回数を増やすほど真の値へと近づいていくことが分かる

数値解析で求めた解はあくまで近似値なので、真の解である数値(真値)との間には誤差が発生する。
誤差 ＝ 近似値 － 真の値

1. 絶対誤差
   真の値と近似値との差
   絶対誤差 ＝ | 近似値 － 真の値 |
2. 相対誤差
   真値に対する誤差の比率
   相対誤差 ＝ 絶対誤差 / 真の値 ＝ | 近似値 － 真の値 | / | 真の値 |
3. 打切り誤差
   計算処理を続けることができなくなり、途中で計算をやめることにより生じる誤差
4. 丸め誤差
   計算値をどこかの桁で端数処理を行ったときに生じる誤差
   端数処理・・・切り上げ・切り捨て・四捨五入など

1. 平成23年度春期　問02　　相対誤差
2. 平成20年度春期　問06　　ニュートン法
3. 平成12年度春期　問09　　誤差
4. 平成11年度春期　問70　　誤差