論理演算とは、複数の条件の組み合わせを条件式で表した時の演算のこと
真と偽の値を持つものの間の演算で、結果もまた必ず真又は偽となるものである。

●論理積(AND) 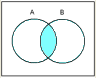両方のビットが「1」の時、 結果が「1(真)」となる。 A = 1 でかつ B = 1 の時だけ 1 になる。
●論理和(OR) いずれかが「1」の時、結果が「1(真)」となる。 A = 1 または B = 1 の時 1 になる。
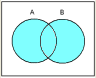●論理否定(NOT) 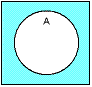ビットを反転させる。 A = 1 の時 0 になる。
●排他的論理和(EOR、XOR) 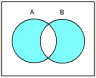ビットが等しければ、「0」、等しくなければ「1(真)」となる。 A = 1 かつ B = 1 の時か A = 0 かつ B = 0 の時 1 となる。
●否定論理積(NAND) 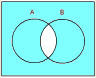ANDの結果の否定 A = 1 かつ B = 1 の時だけ 0 になる。
●否定論理和(NOR) 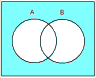ORの結果の否定 A = 1 または B = 1 の時 0 になる。

※論理演算の表現は、「ベン図」「真理値表」「MIL記号」などを使用します。

真理値表

• ANDは、入力の少なくとも1つが「0」のとき、出力は「0」になる。
• NANDは、入力の少なくとも1つが「0」のとき、出力は「1」になる。
• ORは、入力の少なくとも1つが「1」のとき、出力は「1」になる。
• NORは、入力の少なくとも1つが「1」のとき、出力は「0」になる。

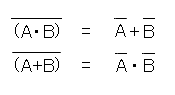●「・」は論理積 (AND) ●「＋」は論理和 (OR) ●「－」は否定 (NOT)

• 積の否定は、否定の和に等しい。
• 和の否定は、否定の積に等しい。

A	B				＋		・
0	0	1	1	1	1	1	1
0	1	1	0	1	1	0	0
1	0	0	1	1	1	0	0
1	1	0	0	0	0	0	0

【 べき等則 】
A ・ A ＝ A
A ＋ A ＝ A

【 交換則 】
A ・ B ＝ B ・ A
A ＋ B ＝ B ＋ A

【 結合則 】
A ・ ( B ・ C ) ＝ ( A ・ B ) ・ C
A ＋ ( B ＋ C ) ＝ ( A ＋ B ) ＋ C

【 分配則 】
A ・ ( B ＋ C ) ＝ ( A ・ B ) ＋ ( A ・ C )
それぞれの積は、展開した和に等しい。
A ＋ ( B ・ C ) ＝ ( A ＋ B ) ・ ( A ＋ C )
それぞれの和は、展開した積に等しい。

【 吸収則 】
A ・ ( A ＋ B ) ＝ A
A ＋ ( A ・ B ) ＝ A

【 その他 】
A ・ 0 ＝ 0
A ・ 1 ＝ A
A ・ A ＝ A
A ・ ＝ 0
A ＋ 0 ＝ A
A ＋ 1 ＝ 1
A ＋ A ＝ A
A ＋ ＝ 1

※＋ = ∪ (和集合), ・ = ∩ (積集合), Ω = 1 (全体集合) , Φ = 0 (空集合) で置き換えれる。

論理演算を利用すると様々な形でビットを操作することができる。

●論理積演算を利用すると元のビットの 1 に対応する部分だけを取り出すことができる。

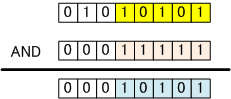
●排他的論理和演算を利用すると元のビットを反転させて取り出すことができる。

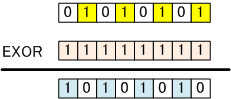
●ビット操作の手法

• 特定の部分をそのまま残して残りはすべて 0 にする
  残す部分を 1 、その他を 0 にしたマスクで AND演算
• 特定の部分をそのまま残して、残りはすべて 1 にする
  残す部分を 0 、その他を 1 にしたマスクで OR演算
• 特定の部分のビットを反転させる
  反転する部分を 1 、その他を 0 にしたマスクで EXOR演算

入力値を元に論理演算の結果を出力する関数のこと。

半加算機・全加算機

1. 平成30年度秋期　問02　　論理演算
2. 平成28年度秋期　問01　　論理演算
3. 平成27年度春期　問01　　論理演算
4. 平成26年度春期　問02　　ビット演算
5. 平成26年度春期　問03　　論理演算
6. 平成25年度春期　問01　　論理演算　ビットシフト
7. 平成25年度秋期　問25　　論理回路
8. 平成23年度春期　問01　　ド・モルガン
9. 平成23年度秋期　問26　　論理回路
10. 平成22年度春期　問02　　論理演算