いくつかの数を、縦横に長方形状にならべて、丸カッコでかこんだものを、行列という。ならべた各数を、その行列の要素（または成分、または元という。 行列で、要素の横のならびを行 (row)、縦のならびを列(column) という。要素の横のならびを、上から順に、第1行、第2行、…といい、要素の縦のならびを、左から順に第1列、第2列、…という。 第i行と第j列の交点にある要素を、(i,j)-要素という。

行列に含まれる行の数が m、列の数が n である時に、その行列を m 行 n 列行列や m×n 行列と呼ぶ。行列を構成する行の数と列の数を合わせて型という。したがってm 行 n 列行列のことを (m, n) 型行列などと呼ぶこともある。

行列同士の和や差の計算は、同じ場所にある数字同士の和や差を求めればよい。

和

差

行列同士の掛け算は、行列の積を前の行列の行（行ベクトル）と後の行列の列（列ベクトル）のそれぞれの数字を掛けて和を取るものと取り決める。従って、前の行列の列の数と後の行列の行の数が等しくなければ計算できない事になる。

積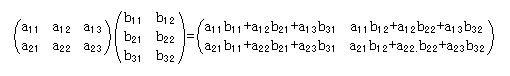

【 正方行列 】
行数と列数が同じ行列のこと

【 単位行列 】
任意の正方行列 A に対して
AE = EA = A
となる行列 E を単位行列という。

2行2列の正方行列の単位行列

3行3列の正方行列の単位行列

である。

【 正則行列 】
任意の正方行列 A に対して
AB = BA = E
となる行列 A を正則行列という。
B を　A の逆行列といい、A^-1で表す。
AA^-1 = A^-1A = E

【 逆行列 】
2行2列の正方行列

の逆行列は、

ad -bc ≠ 0

のとき存在し，

である

【 転置行列 】
行列Aの行と列を入れ替えてできる行列を行列Aの転置行列といい^tAで表す．

【 スカラー値 】
大きさのみの値
例、質量、面積、長さ、温度

【 ベクトル値 】
大きさと向きをもつ値
例、運動量、速度、加速度

【 固有値・固有ベクトル 】
正方行列 A に対して、λ(スカラー値)、x(ベクトル) が、
Ax = λx
を満たす時

• λ を A の固有値
  
• x を A の固有地 λ に属する固有ベクトル
  

と呼ぶ。

例
A が

の時、

x が

の時、固有ベクトルで、λ = 2 が固有値。

x が

の時、固有ベクトルで、λ = 5 が固有値。

a ＞ 0 、a ≠ 1 とするとき、どのような正の数 R に対しても

a^x ＝ R

を満たす実数 x が、ただ1つ定まる。
この x の値を、a を底とする R の対数といい、

x ＝ log_a R

a ・・・ 底
R ・・・ 真数
x ・・・ a を底とするRの対数

で表す。R をこの対数の真数といい、

R ＞ 0

である。

対数の定義より、指数と対数の間には、

x ＝ log_aR ⇔ a^x ＝ R

となる関係が成り立つ。

【 対数の法則 】
a ＞ 0 、a ≠ 1 、R ＞ 0 、S ＞ 0 とするとき

• log_a1 ＝ 0
• log_aa ＝ 1
• a^log_aX ＝ X
• log_aRS ＝ log_aR ＋ log_aS
  
• log_aR/S ＝ log_aR － log_aS
  
• log_aR^t ＝ t log_aR
  
• log_aR ＝ log_bR / log_ba
  

【 指数法則 】
a ＞ 0 , b ＞ 0 , r , s は実数とするとき

• a⁰=1
• a¹=a
• a^r・a^s=a^r+s
• a^r/a^s=a^r-s
• (a^r)^s=a^rs
• ab^r=a^r・b^r
• (a/b)^r=a^r/b^r

【 等差数列 】
隣り合う2項の差が常に一定の数列のこと。
例
1, 4, 7, 10, 13, 16, ・・・

項・・・数列のそれぞれのひとつの数字のこと。
初項・・・数列の一番最初の項、第1項のこと
末項・・・項の個数が有限である数列の、一番最後の項のこと
項数・・・項の個数が有限である数列において、項の全部の個数のこと
公差・・・項と隣の項との差のこと

等差数列の公式
● n 番目の項の値を求める公式
a_n = a + ( n - 1 ) d
d は公差

● 等差数列の初項から末項までをすべて足し合わせる公式
初項 a、末項 l、項数 n の等差数列の和 Ｓ_n を求める公式
Ｓ_n = n ( a + l ) / 2 = n ( 2a + ( n - 1 ) d ) / 2
d は公差

【 等比数列 】
隣り合う2項の比が常に一定の数列のこと。左隣の項にある定数(公比)を掛けて右隣の値とするもの。
例
1, 2, 4, 8, 16, 32, 64, 128, ・・・

公比・・・隣同士の比のこと

等比数列の公式
● n 番目の項の値を求める公式
a_n = a₁ r^(n-1)
r は公比

● 等比数列の初項から末項までをすべて足し合わせる公式
初項 a、公比 r、項数 n の等比数列の和 Ｓ_n を求める公式
a. r ≠ 1 の時
Ｓ_n = a ( 1 - rⁿ ) / ( 1 - r ) = a ( rⁿ + 1 ) / ( r - 1 )

b. r = 1 の時
Ｓ_n = an

【 フィボナッチ数列 】
2つ前の項と1つ前の項を足し合わせていくことでできる数列。
数列は、1, 1, から始まり次々足していく
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ・・・

式で表すと
n ≧ 1 の時
a₁ = a₂ = 1
a_n+2 = a_n+1 + a_n

2つの自然数の最大公約数(GCD：Greatest Common Divider)を求めるアルゴリズム(計算手順)の一つ。古代ギリシャの数学者ユークリッドの発見した古典的な方法。

aとbの2つの数(a＞bとする)の最大公約数を求める場合、

1. aをbで割った余りを求め、これをb’とする。
2. 次に、bをb’で割った余りを求め、a’とする。
3. さらに、b’をa’で割った余りを求め…
4. ひとつ前の除数を余りで割り続ける

と交互に相手を割った余りを割っていき、余りが0になった時点の除数(割る方の数、小さい方の数)が最大公約数である。

ユークリッドの互除法の原理
a と b の最大公約数を GCD(a, b) と表す。a > b > 0 とし，a を b で割った時の余りを r >=0 とする。qは商
a = bq + r
このとき次が成立する。
GCD(a,b)= GCD(b,r)
(aとbの最大公約数) = (bとrの最大公約数)

[証明]
aとbの最大公約数をgとする
a = Ag, b = Bg を a - bq = rにあてはめると
Ag - Bgq = r
g(A - Bq) = r
よってgはrの公約数である。
bとrの最大公約数をg'とする。
b = Bg' , r = Rg' より
a = Bg'q + Rg' = g'(Bq + R)
よってg'はaの公約数である。
g'がgより大きいと最初の前提でgはaの最大公約数であるということがおかしくなってしまう。
よって g = g' でどちらも最大公約数である。

Ex.165と105の最大公約数は
165 ÷ 105 = 1 ・・・ 60
105 ÷ 60 = 1 ・・・ 45
60 ÷ 45 = 1 ・・・ 15
45 ÷ 15 = 3 ・・・ 0
割り切れたので、165と105の最大公約数は15

エラトステネスのふるいとは、ある自然数 n までの素数をすべて求めるための方法です。
考え方は非常に単純で、1からnまでの数値の一覧表を用意して、明らかに素数である2を残し、その倍数である、4,6,8,…を消していきます。
それが終わると、2の次にある、消えていない数3が次の素数となるので、2の場合と同様に、その倍数である、6,9,12…などを消していきます。
この要領で、次の素数5を残し5の倍数を消し、7…で同様の処理をnまで繰り返していくと、最終的に残った数値は、すべて素数になります。

【 素数 】
1 より大きい自然数で、正の約数が 1 と自分自身のみである自然数のことである。 正の約数の個数が 2 である自然数と言い換えることもできる。 1 より大きい自然数で素数でないものは合成数と呼ばれる。

1. 平成29年度春期　問06　　関数
2. 平成24年度春期　問20　　処理時間
3. 平成23年度春期　問06　　関数
4. 平成23年度秋期　問03　　コンピュータの計算時間
5. 平成19年度春期　問02　　桁数
6. 平成19年度秋期　問05　　処理時間
7. 平成11年度秋期　問03　　n進数　最大値　対数