基礎理論 - 1.基礎理論 - 2.応用数学 - 1.確率と統計
1 確率
複数の異なる要素をもつ集合から要素を取り出し、それを取り出した順に並べたものを順列という。
一般に、要素数がn個の場合、それを並べる並べ方(順列の数)は以下の式で表される。
n × (n-1) × (n-2) ×・・・× 3 × 2 × 1
=
n!
また、n個の要素の中からr個の要素を取り出して、それを並べる並べ方は、
nPr
= n! /
(n-r)! (0≦r≦n)
組合せは順列と異なり、要素を取り出した順番は意味を持たない。
一般に、要素数がn個で、その中からr個を取り出す組み合わせの数は、以下の式で表される。
nCr = nPr / r! = n! / (n-r)!r!
※ n!はnの階乗と呼び、1からnまでのすべての整数を掛け合わせることである。
ただし、
1! = 1
0! = 1(0 個のものを並べる順列は「何も並べない」という一通りがあると考えられる)
とする。
階乗を求める関数をf(n)とすると
f(n) = f(n-1)×n (n > 0)
f(n) = 1 (n = 0)
確率とは試行で生じ得るすべての結果に対し、目的とする状態の発生する可能性を表すものである。
偶然性を含まない数で0以上1以下となる。
何度も繰り返し同じ条件でできる事柄を試行と言い、試行の結果起こる事柄を事象と言います。
事象Aの確率P(A)は、事象Aの起こりえる場合の数をn、全事象の数をmとするとき、以下の式で表される。
P(A) = n / m
【 加法定理 】(和事象) (和の法則)
事象AまたはBのいずれかが起こることをいう。
事象Aと事象Bが同時に起こらない(互いに排反である)場合と、両方の事象が重複する部分がある場合の2通りがある。
事象AとBが互いに排反である場合の和事象の確率P(A∪B)は、それぞれの事象の確率の和である。(A または B の起こる確率)
P(A∪B) = P(A) + P(B)
例 サイコロの2,4,6の出る確率
| P(2,4,6) | = P(2) + P(4) + P(6) |
| = 1/6 + 1/6 + 1/6 | |
| = 3/6 = 1/2 |
互いに排反でない場合の和事象の確率は、各事象の確率の和から重複部分の確率を引く( A かつ B の起こる確率)
P(A∪B) = P(A) + P(B) - P(A∩B)
例 サイコロの2の倍数(2,4,6)と3の倍数(3,6)の出る確率
| P(A) | = P(2) + P(4) + P(6) |
| = 1/6 + 1/6 + 1/6 | |
| = 3/6 = 1/2 |
| P(B) | = P(3) + P(6) |
| = 1/6 + 1/6 | |
| = 2/6 = 1/3 |
| P(A∩B) | = P(6) |
| = 1/6 |
| P(A∪B) | = P(A) + P(B) - P(A∩B) |
| = 1/2 + 1/3 - 1/6 | |
| = 4/6 = 2/3 |
全事象(1,2,3,4,5,6)から部分事象(2,3,4,6)の出る確率と同じ
【 乗法定理 】(積事象) (積の法則)
2つの事象AとBが同時に起こることを積事象という。事象が互いに独立し、影響しあわないことを独立事象、一方が他方の事象に影響を及ぼすときは従属事象という。
事象AとBが独立事象である場合、その積事象の確率P(A∩B)は以下の式で表せる。
P(A∩B) = P(A) × P(B)
例 サイコロを2回振ったとき、最初に偶数が出る事象Aと2回目に6が出る事象Bの確率
| P(A∩B) | = P(偶数) × P(6) |
| = 3/6 × 1/6 | |
| = 3/36 = 1/12 |
【 余事象 】
ある事象Aが起こらないことをAの余事象という。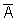 と表す。
と表す。事象Aの発生する確率をP(A)とすると余事象の起こる確率P(
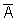 )は以下の式で表せる。
)は以下の式で表せる。P(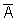 ) = 1 -
P(A)
) = 1 -
P(A)
例 サイコロを3回振って少なくとも1回は1の目が出る確率Aの余事象を考える。事象Aの余事象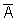 は1が1回も出ないことである。
は1が1回も出ないことである。
P(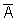 ) ) |
= 5/6 × 5/6 × 5/6 |
| = 125/216 | |
| P(A) | = 1 - P(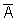 ) ) |
| = 1 - 125/216 | |
| = 91/216 |
このように「少なくとも・・・・・・の確率を求めよ」とあれば余事象を考えてみよう。
【 原因の確率 】
互いに排反であるある事象AとBがあり、そのいずれかの事象により事象Eが発生したとき、その事象Eが発生した原因が事象AまたはBである確率を原因の確率という。
事象Aの発生する確率をP(A)、事象Aが原因で事象Eが起こる確率をP(E|A)、事象Bの確率をP(B)、事象Bが原因で事象Eが起こる確率をP(E|B)とすると、事象Eがおこる原因がAである確率Pは以下の式で表せる。
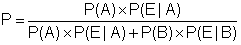 (ベイズの定理)
(ベイズの定理)
Ex どちらのボウルにクッキーがあるか?
クッキーのいっぱい詰まったボウルが2つあるとしよう。ボウル#1には10個のチョコチップクッキーと30個のプレーンクッキーが、ボウル#2にはそれぞれが20個ずつある(これを前提知識とする)。どちらか1つのボウルをランダムに選び、さらにランダムにクッキーを取り出す。結果、クッキーはプレーンだった。これがボウル#1から取り出されたという確率はどれくらいか?
半分以上だというのは直感的にわかる(ボウル#1の方がプレーンクッキーが多いから)。正確な答えをベイズ推定で出そう。H1 をボウル#1、H2 をボウル#2とする。
最初にボウルをランダムに選ぶのだから、そのどちらか一方をとる確率は
P(H1) = P(H2) = 0.5。
「プレーンクッキーが出た」という観察結果を「データD」とする。ボウル1でのD の確率は
P(D | H1) = 30/40 = 0.75
ボウル2では
P(D | H2) = 20/40 = 0.5とわかる。ベイズの式は
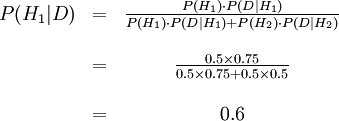
※条件付確率
ある事象B が起こるという条件の下で別の事象A の起こる確率をいい、これをP(A|B)またはPA(B)と書く。
ある集団において、特性 A を持つものの割合が p であり、持たないものの割合が q であるとする( p + q = 1 )。このとき、集団から無作為に n 個を抽出したとき、特性 A を持つものが x 個である確率を考える。
n 個のうち x 個が特性を持つ組合せは nCx 通りある( 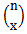 とも書く) 。
とも書く) 。
その各々に対して、x 個が特性 A を持つ確率は px、残り ( n - x ) 個が特性を持たない確率は qn - x であり、両者が共に起こるのは両者の積である。よって、
f ( x ) = nCx px qn - x
x = 0,1, … ,n、
p > 0、q > 0、 p + q = 1 ……(1)
が求める確率であり、この分布を 二項分布 と呼ぶ。
二項分布は、コインを投げて表か裏かのように結果が2つのうちの一つしかないときの、複数回の独立な試行を行ったときの表になる確率分布のこと
(n、p、q は定数である。このようなパラメータのことを 母数 という。n、p を与えることにより、この分布は確定する。p を 母比率 という。この分布を B ( n, p ) と表すことにする。)
Ex. 硬貨を5回投げたときに表が2回出る確率は?
p=1/2, n=5, x=2を公式に当てはめる
P(2)=5C2(1/2)2(1-1/2)5-2
P(2)=(5!/(5-2)!2!)(1/4)(1/8)=5/16
二項分布の平均 E ( x ) と分散 V ( x ) は
である。
ところで、1 回ごとの事象の生起確率 p が一定であるとき、実験を繰り返し行うことを ベルヌーイ試行 というが、独立に実験を n 回繰り返したとき、x 回事象が生じる確率は二項分布である。このため二項分布は ベルヌーイ分布 とも呼ばれる。
ある試行で、その特性を示す値の生起する確率が定まる場合、この特性を示す変数Xを確率変数と言い、確率変数のとる全ての値に対する確率を網羅したものを確率分布と言います。確率分布には離散型確率分布と連続型確率分布があります。
期待値とは、ある事象がおこる確率と確率変数をかけたもの。
【 標準偏差 】
データがどのように分布しているかを見るには散らばり具合(ばらつき or 分布 or 散布度)を調べる。
データの散布度を示すものとして、データの平均値との差 (偏差) の2乗を平均し、平方根をとった標準偏差がある。
標準偏差はデータの分布の広がり幅 (ばらつき) をみる一つの尺度である。平均値と標準偏差の値が分かれば、データがどの範囲にどのような割合で散らばっているか (分布) がある程度明らかになる
標準偏差はデータの分布の広がり幅 (ばらつき) をみる一つの尺度である。
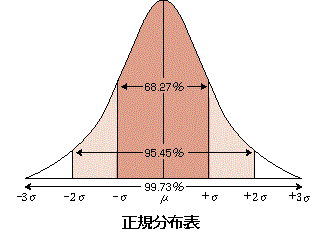
平均値と標準偏差の値が分かれば、データがどの範囲にどのような割合で散らばっているか (分布) がある程度明らかになる。図のような平均値μを中心に左右対称の釣り鐘型の分布 (正規分布) では、平均値 (μ) と標準偏差 (σ) 及び度数の間に次の関係が成り立っている。
【 二項分布 】
繰り返し行われる独立試行で、もし各々の試みに対して単に 2 つの結果だけが可能で、それらが起こる確率が各試行を通じて一定である場合、その試行をベルヌーイ試行といいます。成功の確率が p で失敗の確率が q = 1 - p であるベルヌーイ試行を n 回行った結果、x 回成功する確率(確率関数)は以下のようになり、この分布を母数 p の二項分布と呼びます。
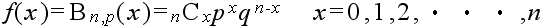
平均 = n p
分散 = n p q
ちなみに二項分布の試行のことを「ベルヌーイ試行」と呼ばれている。
【 ポアソン分布 】(poisson分布)
二項分布に対し、試行の回数nを極限まで大きくし(n→∞)、確率pを0に近づけたとき(p→0)の確率分布を「ポアソン分布」と呼ぶ。一定時間内にごくまれに起こる事象の確率分布のこと。このポアソン分布は、このような性格から、「まれに起こる現象」によく適合する。すなわち、パラパラと発生する事象に適し、集中的に発生する事象には適していない。たとえば、「飛行機に乗って墜落死する確率を求める」といった問題などにはよく適合する。
客の到着時間間隔が指数分布である時、単位時間に到着する客の数に注目した場合の分布などである。
- 定常性・・・同じ幅をもった時間区間あたりの到着の仕方は、時刻に依存しない。
- 独立性・・・共通部分のない時間区間たちのそれぞれの到着の仕方は独立である。
- 希少性・・・同時刻に2人の客がやって来ることはない。
単位時間中にある事象が発生する平均回数を λ とするとき、単位時間中にその事象が x 回発生する確率 P(x) は、ポアソン分布に従う。
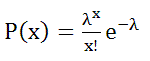 eは自然対数の底=2.178
eは自然対数の底=2.178
指数分布とポアソン分布の関係
ある事象が一定時間内に生じる頻度がポアソン分布に従うとき、その事象の生じる時間間隔は指数分布をとる。
ポアソン分布は、単位時間内に事象の起こる確率であり、指数分布は事象の起こる間隔です。同じ事象を逆の視点で見ていることになります。それで、指数分布の平均は1/λになります
【 指数分布 】
客の到着やサービス時間が偶発的でランダムであるような、一定時間内に起こる事象の時間間隔分布のことをいう。
- 進行中のサービスが終了する確率は、それまでサービスに要した時間に依存しない(マルコフ性と呼ばれます)。
- ある時刻に開始されるサービスは、それ以前に行なわれたサービスや到着に依存しない。
【 正規分布 】
データの分布状態をグラフで表したときに、グラフの形が正規曲線と呼ばれる形になるような分布のことをいう。
正規曲線は、平均値を中心として左右対称になって釣鐘状の形になっている曲線のこと。
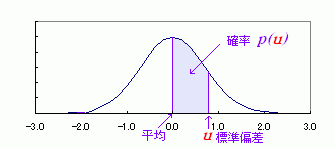
正規分布では、平均±標準偏差の間に、全体の約 68.3 %のデータが含まれる。また、±標準偏差の2倍の範囲内に全データの95.45%が分布する。
平均が 0 、標準偏差が 1 である正規分布を標準正規分布という。
●標準正規分布
正規分布において平均mが0、分散δ(標準偏差)が1の場合を標準正規分布という。
連続分布の中で最もよく現れる代表的なものは正規分布 (Normal Distoribution)です。正規分布は様々な数多くの現象に対してあてはまり、統計学においてとても重要な分布です。分布曲線は正規分布に限らず数多く存在しますが、なかでもこの正規分布は分布の基本といえます。
正規分布は平均値と分散 (標準偏差2) によって完全に決定される分布です。平均値と分散が正規分布を決定するパラメータになります。このことより、正規分布をN (平均値 , 分散) と表記することがあります。
正規分布 N (平均値 , 分散) に従う x を基準値 (標準変化量or確率変数) に変換するとその分布は N(0,1) という分布に従います。
確率分布を標準正規分布表から求めるには、データxについて標準化を行う。以下の式を使う。
基準値(確率変数) = ( x - (平均値) ) / 標準偏差
マルコフ過程
- ある時刻における状態Xtが、その直前の状態だけに依存し、それ以前の状態に依存しない。
将来の状態は現在の状態のみで定まり、過去とは独立している。 - システムの挙動を解析するためには大変有効な性質
- 状態の遷移を、条件付確率で表現できる
2 統計
集められたデータを階級に分け、各階級ごとのデータの数を表の形式で表したもの。
| 得点(点) | 人数(人) |
| 40~50 | 3 |
| 51~60 | 9 |
| 61~70 | 19 |
| 71~80 | 16 |
| 81~90 | 8 |
| 91~100 | 5 |
| 合計 | 60 |
度数分布グラフの1つで、データを任意の区間・階級に区分し、各区間のデータの数を長方形の大きさで示したグラフのこと。資料におけるデータ分布の傾向(ばらつきや偏り具合)把握や異常値の発見に便利である。

(1) データの代表値とは、データ全体の特性を表わす値のこと。次の3つがある。
-
【 平均値 】
データ個々の値を合計したものをデータの個数で割ったもの
データ合計 ÷ データの個数
【 中央値 】
メジアンとも呼ばれ、データを順に並べた時の中央に位置する値
データが偶数個の場合は、中央が 2 つ存在することになるので、その平均をとる。【 最頻値 】
モードともよばれ、データの中で出現回数の最も多い値のこと。
(2) データの散布度とは、個々のデータが平均値の周りにどのように分布しているかの度合いを数値で表したもの。以下のものがある。
【 範囲 】
レンジともよばれ、データの中で最大値から最小値を引いたもののこと。
【 分散 】
平均との差の 2 乗を合計したものをデータの個数で割ったもの
(データの値 - 平均)2の合計 ÷ データの個数【 標準偏差 】
データのばらつきの度合いを表す。 分散の平方根のこと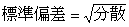
相関関係とは、何らかの関係にある2つの変数の関連性の強さを表現するためのもの。相関関係を数値で表したものを相関係数という。
相関係数 r の範囲は -1 ≦ r ≦ +1 であり、r > 0 の場合を正の相関、r < 0 の場合を負の相関という。
相関係数 r の値が -1 あるいは +1 に近づくほど強い相関があり、0 に近づくほど弱い相関となる。なお r = 0 の場合を無相関といい、2つの変数間に相関がないことを示す。
また、r = ±1 の場合を完全相関といい、このときすべてのデータは一直線(回帰直線)上に並ぶ。
| 強い正の相関 | 右上がりの直線の周辺にデータが集まっている。 | +1 に近い。 | 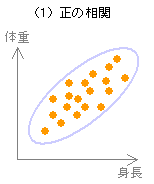
|
| 相関が弱い | 特定の傾向がなく散らばっている。 | 0 に近い。 | 
|
| 強い負の相関 | 右下がりの直線の周辺にデータが集まっている。 | -1 に近い。 | 
|
|
±0.7~±1 |
強い相関がある |
|
±0.4~±0.7 |
中程度の相関がある |
|
±0.2~±0.4 |
弱い相関がある |
|
±0~±0.2 |
ほとんど相関がない |
【 回帰分析 】
相関関係にある2つの変数の関係を数式で表現し、データを分析・予測する統計的手法。または、要因と結果の2つの数値の因果関係を分析するための統計的手法。
2つの変数のうち、値がわかっている変数(要因となる数値)を説明変数、その値を基に予測したい変数(結果となる数値)を目的変数(被説明変数)という。
説明変数がひとつの場合を、単回帰分析といい、2つ以上の場合を重回帰分析という。
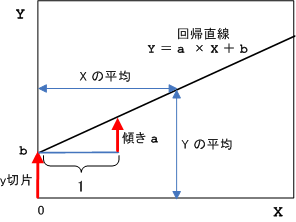
データの散らばり具合が直線的であれば、その傾向を一次式で表す。この直線を回帰直線という。
回帰直線は各点からの距離の2乗の和が最小となるような直線とする。これを最小2乗法という。
回帰直線の性質として、データ x の平均 X と y の平均 Y を必ず通る。
【 ロジスティク回帰分析 】
一つのカテゴリ変数(二値変数)の成功確率を、複数の説明変数によって説明、予測する多変量解析の一つ。
[追加] 回帰分析(単回帰分析, 重回帰分析, ロジスティク回帰分析), 相関分析, 主成分分析, 因子分析
データが多く、すべてのデータを調査することが困難な場合、いくつかのデータを取り出し、それを元に全体の平均・分散などの傾向を算出すること。
全体のデータのことを母集団、いくつかの元になるデータのことを標本という。
- 平成30年度春期 問02 組み合わせ
- 平成28年度春期 問54 顔合わせ会
- 平成28年度秋期 問02 確率
- 平成27年度春期 問03 期待値
- 平成27年度春期 問04 遷移確率
- 平成27年度秋期 問02 組み合わせ
- 平成26年度春期 問04 正規分布
- 平成23年度春期 問67 期待需要
- 平成22年度春期 問41 パスワード
- 平成22年度春期 問76 相関係数 回帰直線
www.it-shikaku.jp