基礎理論 - 1.基礎理論 - 1.離散数学 - 3.算術演算と精度

Last Update : January 02 2021 16:00:14

　 　 　

a. 表現可能な数値の範囲

【 固定小数点数 】
●符号なし整数のみの場合。

8ビット ・・・ 28 = 0 ～ 255
16ビット ・・・216 = 0 ～ 65,535
32ビット ・・・232 = 0 ～ 4,294,967,295
nビット ・・・2n = 0 ～ 2n

●符号つき整数のみの場合。負数は 2 の補数
8ビット ・・・ － 27 ～ 27 － 1 = － 128 ～ 127
16ビット ・・・ － 215 ～ 215 － 1 = － 32,768 ～ 32,767
32ビット ・・・ － 231 ～ 231 － 1 = － 2,147,483,648 ～ 2,147,483,647
nビット ・・・ － 2n－1 ～ 2n－1 － 1


b. シフト演算

元の数字を左右にシフトすることで、乗算や除算が可能になる。
左へ 1 ビットシフトすると元の数字を 2 倍したことになる。2 ビットシフトすると 22倍したことになる。
右へ 1 ビットシフトすると元の数字を 1/2 倍したことになる。2 ビットシフトすると 1/22倍したことになる。

  • 左に n ビットシフト ＝ 元の数字を 2n 倍
  • 右に n ビットシフト ＝ 元の数字を 2-n 倍 ＝ 1/(2n) 倍

0 0 0 0 1 0 1 1 ＝ 23 ＋ 21 ＋ 20 ＝ 11(10)
　　
0 0 0 1 0 1 1 0 ＝ 24 ＋ 22 ＋ 21 ＝ 11(10) × 2 ＝ 22(10)
　　
0 0 1 0 1 1 0 0 ＝ 25 ＋ 23 ＋ 22 ＝ 11(10) × 22 ＝ 44(10)
　　
0 1 0 1 1 0 0 0 ＝ 26 ＋ 24 ＋ 23 ＝ 11(10) × 23 ＝ 88(10)
　　
1 0 1 1 0 0 0 0 ＝ 27 ＋ 25 ＋ 24 ＝ 11(10) × 24 ＝ 176(10)


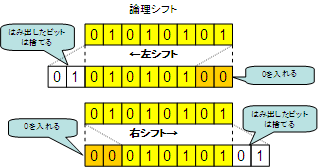
【 論理シフト 】
論理シフトは単純にビットを右または左にずらすことです。
はみ出したビットは捨てます。足りないビットには 0 を補います。

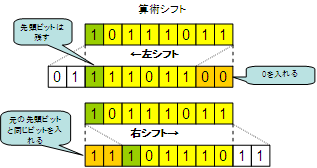
【 算術シフト 】
算術シフトは、符号を考慮してビットをずらします。
左シフトの場合、先頭ビットは残してずらす、右の足りないビットには 0 を入れる。 右シフトの場合は、左の足りないビットは、元の先頭ビットと同じものを入れる。

算術シフトの負数は 2 の補数で表現する。
算術シフトは、左シフトでビットをずらすとき、あふれが生じる。あふれの判断は、
元の数が正数のとき、左シフトで 1 が消えたときあふれとなる。
元の数が負数のとき、左シフトで 0 が消えたときあふれとなる。


c. 誤差

【 丸め誤差 】(仮数部で発生する誤差)
コンピュータでは、計算に利用するビットの桁数が決まっているので、計算する値がそのビット数をオーバーするため、ある桁数で、切り捨てや四捨五入をすることで誤差が生じる。その誤差を丸め誤差という。
10 進数の 0.2 を 2 進数になおすと、 0.0011001100110011… と無限小数になってしまう。
これを仮数部を 23 ビットで表すと、24 ビット以降が切り捨てられてしまう。
そのため、その 2 進数を元の 10　進数に戻しても、ぴったり 0.2 に戻らない。
これが丸め誤差になる。

【 けた落ち 】(仮数部で発生する誤差)
絶対値のほぼ等しい二つの数値を減算したときに、有効桁数が減少してしまうことをいう。
たとえば、0.1235 － 0.1234 ＝ 0.0001になる。これを正規化すると、0.1 × 10-3になり、0.1235 と 0.1234は、本来有効桁数は 4 桁であったけれど、0.1 × 10-3は有効桁数は 1 桁になってしまう。

【 情報落ち 】(仮数部で発生する誤差)
絶対値の差が非常に大きな二つの数値の加減算を行う時に、絶対値の小さいほうの値が計算結果に反映しないために起こる誤差
たとえば、どちらも有効数字 3 桁の 0.123 × 106 ＋ 0.124 × 10-6　を計算すると 123000 ＋ 0.000000124 ＝ 123000.000000124 ＝ 0.123000000000124 × 106になる。 これを有効数字 3桁と考えると 0.123 × 106になり、0.124 × 10-6の値がなくなってしまう。
情報落ちをなるべく起こらないようにするには、計算を連続して行う場合に、絶対値の小さなものから順番に計算していくことで情報落ちを避けることができる。

【 打ち切り誤差 】
計算を途中で打ち切ることによって生じる誤差をいう
コンピューターで数式などの解を求める際に、計算を繰り返し実行させることで値を近似させるとき、ある一定時間を超えたところで演算は終了される。そのようにして得られた値と真の値との間に生じた誤差が、打ち切り誤差と呼ばれる。

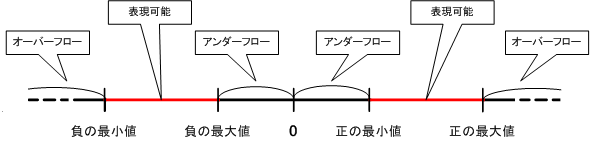
【 オーバーフロー（あふれ） 】(指数部で発生する誤差)
絶対値の大きなもの同士の乗算で、桁数が足りなくなってしまうことをいう。
指数部での表現ができなくなってしまうこと。

【 アンダーフロー 】(指数部で発生する誤差)
絶対値の小さなもの同士(非常に 0 に近い)の乗算を行うことで、表現できなくなってしまうことをいう。
指数部での表現ができなくなってしまうこと。


　　[ 例題 ]　
  1. 平成29年度春期　問05　　シフト演算
  2. 平成29年度秋期　問01　　ビットシフト
  3. 平成28年度秋期　問04　　2進数　ビットパターン
  4. 平成27年度春期　問02　　誤差　けた落ち
  5. 平成26年度秋期　問03　　2進数　ビットパターン
  6. 平成25年度秋期　問02　　論理シフト
  7. 平成24年度秋期　問01　　算術シフト
  8. 平成23年度秋期　問02　　８ビット固定小数点形式
  9. 平成22年度秋期　問02　　誤差　けた落ち
  10. 平成21年度春期　問01　　シフト演算


　 　 　

www.it-shikaku.jp