基礎理論 - 1.基礎理論 - 4.通信に関する理論 - 1.伝送理論
【 位相・振幅・周期(周波数) 】
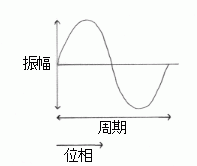
振幅は波の高さを表します。周期は下図の矢印内の期間を、一周期という(周期=1/周波数)。そして、一周期内の波の位置を、位相という。
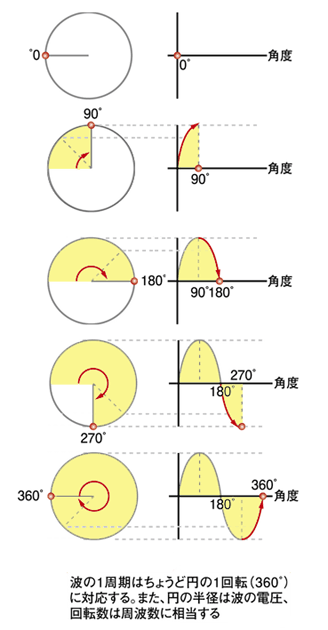
これら三つは変調を理解する上で、非常に重要な要素です。特に位相は角度で表され、一周期のスタート点を 0゜とし、最後の部分を 360゜として扱う。
【 単方向 】
単方向通信とは、決まった方向にしか通信しない方式である。
【 半二重 】
双方向の通信ができるが、送信時には受信ができず、受信時には送信ができない、同時に双方向の通信はできない。。
【 全二重 】
双方向の通信ができて、送信と受信を同時に行うことができる。
ここで、「単方向モード」「半二重モード」の場合は、「2線式」が必要で、「全二重モード」の場合は「2線式の多重化」か「4線式」を使用します。
伝送路に電気信号を流す方式としては、デジタル信号をそのままの形で伝送路に流す ベースバンド方式 と、デジタル信号をアナログ信号に変調(データを決まったキャリア(搬送波)に載せて伝送する方式)して流す ブロードバンド方式 があります。
- ベースバンド方式は、伝送路の物理的な影響を受けやすく遠距離通信に向いていないという面はありますが、非常に単純な方式で、現在の LAN のほとんどがこの方式を採用しています。 ただし、同時に複数の通信を行なうことができないというデメリットもあります。
- ブロードバンド方式は、デジタル信号をアナログ信号に変換して送信し、受信側でアナログ信号を再びデジタル信号に戻す、いわゆる変調・復調という作業を伴う伝送方式です。電話回線を使用してインターネットにアクセスする場合は、この伝送方式になります。 この方式は、伝送路の物理的な影響を受けにくく、遠距離通信に向いているという特徴があります。
現在私たちが利用するPCをはじめとしたコンピュータは、処理する情報のすべてを、"0"もしくは"1"で構成されるデジタル信号として認識し、計算を行っている。このため、コンピュータ間におけるデータのやり取りは、デジタル信号でそのまま行うと都合が良い。
ところが伝送路には、電話回線網における電話と局間を結ぶアクセス網部分のように、音声などのアナログ信号しかやり取りできないものも存在する。このため、コンピュータによって出力されたデジタル信号をアナログ信号へ変換して送信したり、受信したアナログ信号をデジタル信号へ変換してコンピュータに渡したりするメカニズムが、どうしても必要となる。これらを実際に行っている機器がモデムである。
なお、デジタル信号をアナログ信号へと変換することを変調(modulation)という。また、受信信号から元の情報を復元する動作を復調(demodulation)という。
ちなみにモデムとは、変調機(modulator)と復調機(demodulator)の双方の機能を持つ機器であることから、その合成語としてMODEMと呼ばれている。
【 振幅変調方式 】
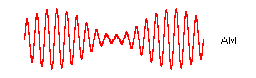
AM ( Amplitude Modulation :振幅変調 ) は、アナログ信号の振幅によって伝送する方式
振幅に強弱をつけ、この違いにそれぞれ0または1を割り当てることで、ビットデータを転送できるようにする。
【 周波数変調方式 】
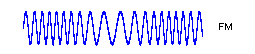
FM ( Frequency Modulation :周波数変調 ) は、アナログ信号の周波数によって伝送する方式
周波数を変化させることで、異なる周波数に0または1を割り当て、ビットデータを転送できるようにする。
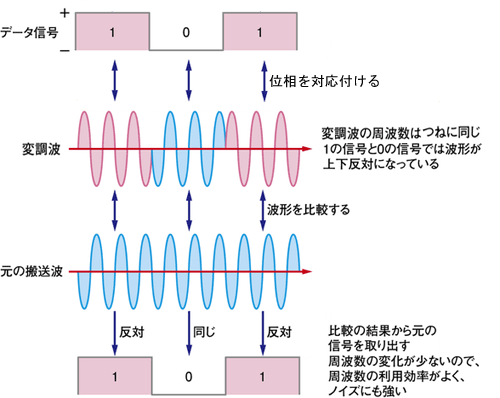
【 位相変調方式 】
PM ( Phase Modulation :位相変調 ) は、アナログ信号の位相の違いによって伝送する方式
データによって搬送波の位相をずらして利用するのが「位相変調(PM:Phase Modulation、PSK:Phase Shift Keying)」で、デジタルデータととても相性がよい。そのため、無線LANを始め、無線を使うデータ通信の世界ではほぼ標準的な変調方法として使われている。
位相とは、波の1つの周期の始まりを0°、終わりを360°とする。これは、もっとも純粋な波である「サインカーブ(正弦波)」がひもでつないだボールを回転させたときのボールの高さをトレースした曲線であることに由来する。
周波数変調に比べて、装置は若干複雑になる。同一雑音下での伝送効率は位相変調の方が優れているが、伝送帯域当たりの効率がよくないため、現在はあまり使われていない。
【 パルス符号変調方式 】
PCM ( Pulse Code Modulation :パルス符号変調 )は、アナログ信号を標本化(サンプリング)・量子化し、得られた信号の大きさを二進の数値データとして表現する。このため、他のパルス変調法に比べ、計算機による処理を行いやすい利点がある。
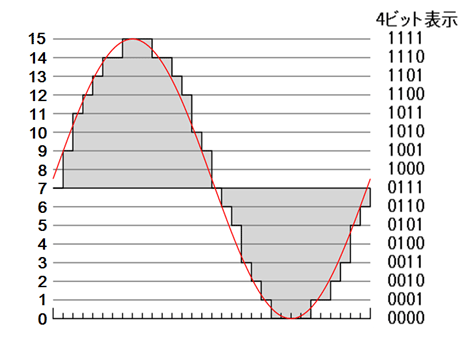
振幅をパルス列のコードに変換します。上の図は、振幅を16レベルに分類し4ビット(4つの1、又は0で現わす)のコードに変換します。実際のレベルは、それぞれの時間に対して図の右側に示す「4ビット表示」の値に変換されて表示されます。
通信を行う端末が複数ある時、それぞれに伝送路を確保すると費用がかかる。そのため、1 本の伝送路を使って同時に複数の信号を行うことを多重化という。
【 周波数分割多重方式 】
FDM ( Frequency Division Multiplexing :周波数分割多重 ) は、ある間隔だけ離れた複数の周波数を使って多重化する方式。
送信元では、異なる周波数の波を合成して信号を伝送する。受信側では、この波から周波数の異なる波に分解して取り出す。
アナログ回線で利用される。
【 時分割多重方式 】
TDM ( Time Division Multiplexing :時分割多重 )は、伝送路を一定の時間毎に切り替えて多重化する方式。
複数の端末に順番に一定時間ずつ伝送する。ディジタル回線で利用される。
【 波長分割多重方式 】
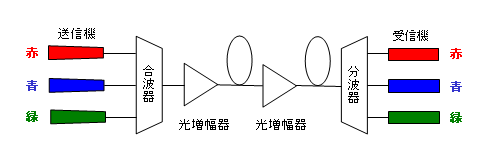
WDM (Wave Division Multiplexing:波長多重方式)は、少ない光ファイバ回線で、大量のデータを高速に伝送させるための技術です。
それまでの光通信は、一つの光ファイバに一つの光を通し、これを点滅させて信号を送っていました。WDMは、同じ光ファイバに別の光も一緒に入れて送ります。
もちろん、波長が同じであると識別できないので、別の波長の光を入れてやります。
赤や青や緑 (実際には可視光ではないのでこのような色はない)といった光を個別に点滅させ、これを1本の光ファイバで伝送します。こうすれば、光ファイバを増やさなくても容量を数倍、数十倍にできるという技術です。
ディジタル信号の伝送・記録では、1ビットの誤りが致命的な問題を引き起こす可能性があります。
このため、フロッピーディスクやHDD・CD-ROM・DVDの記録媒体や、モデム・Ethernetなどのネットワークの分野では、これらの誤りを検出するため仕組みがあります。
【 CRC 】(巡回冗長検査)
巡回符号(Cyclic Redunduncy Code)は線形符号の一種で、複数ビットの連続(バースト)誤り検出に強い符号です。パリティのように 1 ビットの誤りしか訂正できない方法に比べて信頼性が高い。通信やディスクの誤り検出に広く利用されています。通常は、ビット列を多項式と見なして、「生成多項式」とよばれる定数で割った余りを求めます。生成多項式には、X16+X12+X5+1などが使われる。
- 1 ビット以上の誤りを検出できる。
- 高速である。
- パリティ・チェックサム方式に比べ検出精度が高い。
- 1ビットずつの走査により計算ができ、チェックするためのハードウェア回路が簡単。
送信データのビット列を多項式として、それを決められた生成多項式(16bitの場合 X16+X12+X5+1)で割り、その余りのビット列を送信データに付加して送信します。受信側ではその逆算を行って誤りを検出します。非常に高い精度で誤り検出が可能です。特に通信では連続的にビット誤りが発生します。それをバースト誤りといいますが、その検出に効果的です。CRCはHDLCでの誤り制御に採用されているので、LANやインターネットで広く用いられている仕組みです。
● CRCの仕組み
CRC 方式は、受信したデータを多項式に直したものを S(X) とするとき、 S(X) が 生成多項式 G(X)で割りきれるとき受信データは正しい。 (割り切れない場合、受信データに誤りがある)。
データビットを多項式で表す場合は、右側から数えて n ビット目に 1 が立っていたら X(n-1)に直して、それぞれを加えます。
元のデータの多項式を D(X) とするとき、CRCを付加したデータの多項式 S(X) は
S(X) = Xk・D(X) + R(X)
(k はチェックビットの長さ。チェックビットを加える分だけ元のデータを左側にずらす。)
R(X) は Xk・D(X) を G(X) で割った余りでチェックビット(CRC)になる。(生成多項式と同じ次数)
すなわち、
Xk・D(X) / G(X) = 商 Q(X) ・・・余り R(X)
Xk・D(X) = Q(X)・G(X) + R(X)
S(X) = Q(X)・G(X) = Xk・D(X) + R(X)
の関係にある。
本来は、Xk・D(X) - R(X) になるが、モジュロ演算を行うため - R(X) = + R(X) なので Xk・D(X) + R(X)になる。(モジュロ2演算 参照)
生成多項式 G(X) の選択は重要である。多項式は誤り検出機能を高め、かつ CRC値の衝突が起き難くなるよう選択する必要がある。
1. チェックビットの作り方
送信するビット列を10011(多項式に直すとX4+X+1)、生成多項式をX6+X2+1
とする。(1000101)
前もって10011の後ろに生成多項式の次数分の0を付加する。(000000のゼロを付加)
それを生成多項式で割る。
ただし、モジュロ2除算で計算するので、XORで計算する。
10010
-------------------
1000101 ) 10011000000
XOR 1000101
-------------------
1001000
XOR 1000101
-------------------
011010 ← 余り
10011の桁まで商を計算する。余りは011010になる。
CRCを付加して送信するデータは、10011011010になる。
2. 誤り検出符号の確認
生成多項式 : G(X) = X6+X2+1
受信データ : 10011011010
受信データの後ろの 6 ビットがチェックビットであり(チェックビットの大きさは、生成多項式の次数)、先頭の 5 ビットがデータビットである。データビット(伝送データ D(X)) は 10011 であり、多項式で表せば、 D(X) = X4 + X + 1 となる。
このとき、受信データ(10011011010)を多項式で表すと、
S(X) = X10+X7+X6+X4+X3+X
となり、 S(X) を G(X) で割ると
S(X)/G(X) = X4 + X ... 余り 0
10010
-------------------
1000101 ) 10011011010
XOR 1000101
-------------------
1000101
XOR 1000101
-------------------
00
となり割り切れる。したがって、受信データに誤りはない。
【モジュロ2演算】
0+0=0
0+1=1
1+0=1
1+1=0
0-1=1
-0=0
-1=1
これより、 modulo2の演算では、 加算(プラス)と減算(マイナス)に違いはなく、 同じ結果になることがわかります。
modulo2 の変数 x を用いた多項式についても、以下のように加算と減算を行うことができます。
0+x=x
x+0=x
x+x=0
0-x=x
x-0=x
x-x=0
-x=x
【 ハミング符号 】
同一のデータに対して、複数の方法でチェックコードを付加する方式。
1 ビットの誤り検出・訂正を行える。また誤り検出だけなら 2 ビットまで検出できる。
ハミング符号はシンプルで誤りの検出・訂正能力は弱いが高速に処理できるという特徴があり、ECCメモリやRAID-2の誤り検出に利用されている。
● ハミング符号の仕組み
情報ビット4ビット、冗長ビット3ビットからの7ビットのハミング符号で考える。(これを(7,4)ハミング符号という。)
D = (d1, d2, d3, d4, d5, d6, d7)
= (x1, x2, x3, x4, p1, p2, p3)
dをxとpに置き換えて、
冗長ビットを以下のルールで作成する。(以下すべてモジュロ演算)
p1 = x1 + x2 + x3
p2 = x2 + x3 + x4
p3 = x1 + x2 + x4
これは、以下のように置き換えられる。
0 = x1 + x2 + x3 + p1
0 = x2 + x3 + x4 + p2
0 = x1 + x2 + x4 + p3
1. 検査方程式
以上のことから以下が成り立つ
d1 + d2 + d3 + d5 = x1 + x2 + x3 + p1 = 0
d2 + d3 + d4 + d6 = x2 + x3 + x4 + p2 = 0
d1 + d2 + d4 + d7 = x1 + x2 + x4 + p3 = 0
2. シンドロームの計算
受信データから、誤り位置を診断するための情報をシンドロームといい、受信データを上の検査方程式のルールで計算する。
受信データを Y = (y1, y2, y3, y4, y5, y6, y7) とする。
s1 = y1 + y2 + y3 + y5
s2 = y2 + y3 + y4 + y6
s3 = y1 + y2 + y4 + y7
s1~3 は、上の検査方程式のルールで計算されているので、s1~3 がすべて 0 の時、ビットにエラーはない
受信データにエラーがある場合、以下が成り立つ
s1 = (d1 + e1) + (d2 + e2) + (d3 + e3) + (d5 + e5)
s2 = (d2 + e2) + (d3 + e3) + (d4 + e4) + (d6 + e6)
s3 = (d1 + e1) + (d2 + e2) + (d4 + e4) + (d7 + e7)
例えば、
受信データが正しい場合、 d1 が 0 の時、受信後のデータ y1 が 0 になる
y1 = d1 + e1 = d1 + 0 = 0 + 0 = 0
d1 が 1 の時、受信後のデータ y1 が 1 の時
y1 = d1 + e1 = d1 + 0 = 1 + 0 = 1
エラーがない場合の e1~7は0になる。
受信データがエラーの場合、
送信前のデータ d1 が 0 の時、受信後のデータ y1 が 1 の時
y1 = d1 + e1 = d1 + 1 = 0 + 1 = 1
になる。
送信前のデータ d1 が 1 の時、受信後のデータ y1 が 0 の時
y1 = d1 + e1 = d1 + 1 = 1 + 1 = 0
になる。
どちらも 1 が足されることでビットが反転する。
エラーがあった場合、そのビットに 1 が足されたことと同じになる。
よって、エラーがあったビットの e1~7のどれかに1が立つ。
e1~7に1が立っている受信ビットはエラーである。
3. ハミング符号の誤り訂正
1ビット誤りの場合、データは7ビットなので7種類の誤りビットが考えられる。
受信データを使って、シンドロームを計算することで、誤り位置が特定できる。
| e1 | e2 | e3 | e4 | e5 | e6 | e7 | s1 | s2 | s3 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ← この場合、受信データは正しい |
受信データからシンドロームを計算して、オール 0 以外はビットに誤りがある。
s1、s2、s3の並びで、どのビットが誤っているのかがわかる。
誤りがない場合、s1、s2、s3は、それぞれ 0 になる。
[例]
受信データが、0111100の時、誤りビットはどれか。
s1 = y1 + y2 + y3 + y5 = 0 + 1 + 1 + 1 = 1
s2 = y2 + y3 + y4 + y6 = 1 + 1 + 1 + 0 = 1
s3 = y1 + y2 + y4 + y7 = 0 + 1 + 1 + 0 = 0
S = s1s2s3 = 110
上の表より、左から 3 ビット目が誤り。
検証
上のデータを正しいデータ 0101100 (3 ビット目を訂正)にしてシンドロームを計算すると
s1 = y1 + y2 + y3 + y5 = 0 + 1 + 1 + 0 = 0
s2 = y2 + y3 + y4 + y6 = 1 + 0 + 1 + 0 = 0
s3 = y1 + y2 + y4 + y7 = 0 + 1 + 1 + 0 = 0
S = 000
なので、正しい。
【 パリティチェック 】
1 ビットのチェックビット(パリティビット)を用いてデータのエラーを検出する方式。垂直パリティともいう。
1文字ごとにパリティビットを付加します。データを7ビット単位に区切り、最後の1ビットにパリティビットを付加して8ビットにします。
パリティチェックでは1ビットのエラーの検出ができるが訂正はできない。2ビット以上のエラーは検出できない。
- [ 偶数パリティ ]
パリティビットを含めて 1 の数が偶数になるようにするのが偶数パリティ8 7 6 5 4 3 2 1 1 0 1 0 1 0 0 1 ↑ パリティビット - [ 奇数パリティ ]
パリティビットを含めて 1 の数が奇数になるようにするのが奇数パリティ8 7 6 5 4 3 2 1 0 0 1 0 1 0 0 1 ↑ パリティビット
●水平垂直パリティ
ブロックごとに、BCC(Block Check Character)と呼ばれるパリティビットを付加して、データ誤りが発生したかどうかを検出します。
水平パリティの場合、今度は水平方向にパリティチェックを行い、パリティ結果を「BCC」という1文字分のデータを作成します。
水平パリティでは、文字を構成するビットで2ビット以上の誤りに対しても検出できます。また、1ビットの誤りならば訂正も可能。
垂直パリティに奇数パリティ、水平パリティに偶数パリティを設定した場合。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 垂直パリティビット | |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 2 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 3 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 4 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 5 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | |
| 6 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 7 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | |
| 8 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | |
| ↑ 水平パリティビット(BCC) | |||||||||
4件目のデータの3つ目(4行 3列目)のビットが間違っている場合
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 2 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 3 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 4 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | ← 垂直パリティおかしい |
| 5 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | |
| 6 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 7 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | |
| 8 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | |
| ↑ | 水平パリティおか | しい | |||||||
3件目のデータの4つ目と5つ目(3行 4列目・5列目)の2ビットが間違っている場合
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 2 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 3 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | ← 垂直パリティ正しい |
| 4 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 5 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | |
| 6 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 7 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | |
| 8 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | |
| ↑ | ↑ | 水平パリ | ティおかしい | ||||||
【 ECC 】(Error Correcting Code : 誤り訂正符号)
ECCは、データの誤りを検出し、訂正するために本来のデータとは別に付加される冗長なデータのこと。また、そのような機能のこと。
メモリ内のデータのエラーを検出したり、自動的にエラーの訂正ができる。
サーバやワークステーションなどのように高い信頼性が求められる記憶装置やバス(データ伝送路)などで使われることが多い。誤り訂正符号によるエラー訂正方式には、チェック・サム(Check Sum)やCRC(Cyclic Redundancy Check)などがある。
【 チェックサム 】
データを送受信する際の誤り検出方法の一つ。送信前にデータを分割し、それぞれのブロック内のデータを数値とみなして合計を取ったもの。求めたチェックサムはデータと一緒に送信する。受信側では送られてきたデータ列から同様にチェックサムを計算し、送信側から送られてきたチェックサムと一致するかどうかを検査する。両者が異なれば、通信経路上でデータに誤りが生じていることになるので、再送などの誤り訂正手続きをとる。
データの送受信を行うには、送信側と受信側でお互いにタイミングを合わせてデータのやり取りを行わなければならない。タイミングを合わせることを同期という。
【 ビット同期 】
伝送同期方式の1つで、クロック同期ともいう。データ信号とクロック信号のタイミングを合わせることでビット単位で同期を取る方法。
- 同期方式
同期方式では、データ伝送路とは別の伝送路で同期用タイミング信号を送るものと、データからタイミングを分離し抽出するものがある。送信側では、一定のタイミングに同期させて連続的にビット系列を送出する。受信側では、そのタイミングに同期してビット系列を受け取る。
- 調歩同期方式
送信データ 1 文字ごとに、スタートビット( 0 )とストップビット( 1 )をつけて送る方式。
1 文字 8 ビットとしたとき、1 文字送信するのに 10 ビット必要になる。
2 ビット余計に必要になるので高速通信には不向き。RS-232C等のシリアル通信は調歩同期式が使われる。送信方向 ← 0 0 1 1 0 0 1 0 1 1 0 0 0 1 0 1 1 1 1 1 スタートビット ↑ データ ↑ ストップビット 調歩同期式では、あらかじめ送信側と受信側で以下の値を同じにしておきます。
・データサイズ(7ビット or 8ビット)
・パリティビットの有無
・伝送速度(ボーレート)
【 ブロック同期 】
データブロック単位で同期を取る方法で、各データブロックの先頭位置を明示する手段として、特殊なビット列を用いる。
- フラグ同期方式
フレーム同期ともいう。送信データの前後にフラグシーケンスという特殊なビット列(0111 1110)を付加することで、同期をとる方式です。送信がない場合でも、「フラグシーケンス」を常に送信して同期をとり、任意のビット長のデータ伝送に使用されます。
フラグシーケンスと違うビット列が表れたときから次のフラグシーケンスが表れるまでのビット列をひとつのデータとみなします。この方法だと画像データや音声データも送ることができます。
フラグ同期方式では、フラグと同じビット列がデータ中に出現する(1が連続して6つ)のを防ぐため、ゼロインサーションを行います。ゼロインサーションとは、データ中に1が5つ連続して出現した直後に0を挿入することです。受信側は1が5つ連続したあとの0は省きます。そうすることで元のデータに戻すことができます。その上でフラグなのかどうかを判断します。送信方向 ← 開始フラグ アドレス 制御部 データ CRC 終了フラグ - SYN同期(キャラクタ同期)方式
キャラクタ同期ともいう。
送信するデータの前にSYN符号(2進数で0001 0110)という同期用の符号をいくつか(基本2つ)送信し、この符号を確認することで同期をとる方法。
その後は連続してデータを送信する。送信方向 ← SYN SYN 文字 文字 文字 文字 ・ ・ ・ ← データ →
- 平成30年度秋期 問11 冗長ビット
- 平成29年度秋期 問02 パリティチェック
- 平成27年度春期 問10 冗長ビット
- 平成26年度春期 問11 パリティチェック
- 平成25年度春期 問04 パリティチェック
- 平成22年度秋期 問04 誤り制御方式
- 平成20年度春期 問10 パリティビット
- 平成19年度春期 問11 パリティビット
- 平成19年度秋期 問23 パリティ
- 平成18年度春期 問23 誤り制御方式
www.it-shikaku.jp